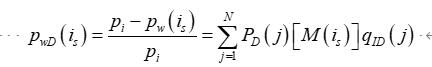产能预测模型中的耦合是指不同场(包括油藏渗流场、油藏温度场等)或流体流动环节(包括油藏渗流、井筒管流、裂缝窜流等)之间的相互影响,协同生产的现象。针对不同的应用场景,常采用不同的耦合方式来提高产能预测模型的精度。
井筒与油藏的耦合是最常见的耦合方式,1990年Dikken等人假设井筒为单相流动,首次建立了考虑井筒流动和地层渗流耦合的水平井模型。2000年,刘想平在Dikken的基础上,充分考虑了水平井筒内变质量流的流动特性,建立了水平井筒与渗流耦合的流动压降计算模型,为产能模型提供了基础。2011年同登科综合考虑了启动压力梯度、储层介质的分形,建立了分形低渗透油藏-井筒耦合流动模型。2011年Bahonar等研究了考虑瞬态非等温的井筒-油藏全耦合模型,该模型充分考虑了气井井筒内流动的复杂性,进一步提高了井筒-油藏耦合产能预测模型的预测精度。乐平等人于2015年采用微元思想,用储层细分的方法代替井筒细分的处理方法,建立了底水油藏鱼骨分支水平井储层渗流与井筒渗流的耦合模型。目前井筒与油藏耦合已经成为不同地质模式下各种复杂井型的产能预测模型中所需考虑的重要手段,有着非常广阔的应用前景。
将油藏看作一个整体,将井筒离散成N段,如下图所示。显然,该产能预测模型为半解析模型。任一段为is,第is段处对应的压力和流入量分别为Pw (is )和q(is )。

井筒离散示意图